From The Sunday Times, 24th April 1983 [link]
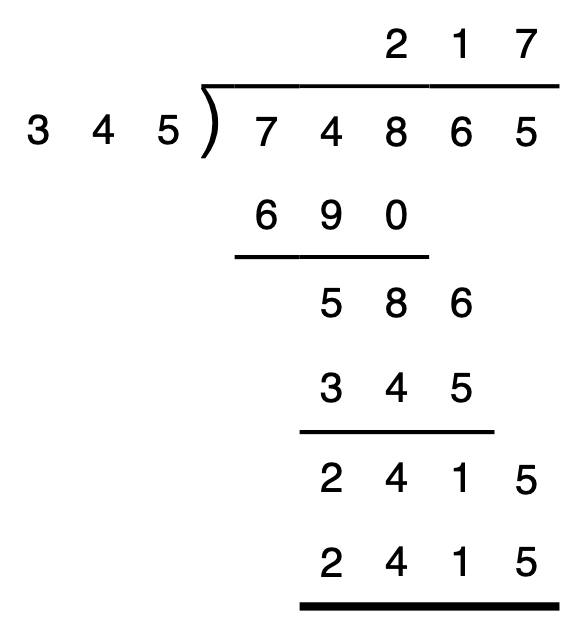
Fred and I usually do the washing and drying up in our commune. Fred always washes the largest saucepan first, then the second largest, and so on down to the smallest. In this way I can dry them and store them away in the order they were washed, by putting one saucepan inside the previously washed saucepan, ending up with a single pile.
Yesterday, the cook misread the quantities for the sherry trifle recipe, with the result that Fred got the washing up order completely wrong. For example, he washed the second smallest saucepan immediately after the second largest; and the smallest saucepan immediately before the middle-sized saucepan (i.e. the saucepan with as many saucepans larger than it as there are smaller).
I realised something was wrong when, having started to put the saucepans away in the usual manner, one of the saucepans did not fit the previously washed saucepan; so I started a second pile. Thereafter each saucepan either fitted in to one, but only one pile, or did not fit into any pile, in which case I started another pile.
We ended up with a number of piles, each containing more than one saucepan. The first pile to be completed contained more saucepans than the second, which contained more than the third etc.
In what order were the saucepans washed up? (Answers in the form a, b, c, …, numbering the saucepans from 1 upwards, 1 being the smallest).
This puzzle is included in the book The Sunday Times Book of Brainteasers (1994).
[teaser1081]




Jim Randell 4:09 pm on 19 July 2024 Permalink |
The smaller two numbers must be 3-digit numbers, and so the remaining number must have 4 digits.
I used the [[
SubstitutedExpression()]] solver, from the enigma.py library, to generate the possible sets of 3 numbers.The sets are then grouped by (<length of product>, <parity of product>), and we look for keys that give a unique set of numbers, such that there is also at least one set grouped under the opposite parity (which means that there are multiple products with the same digit length).
The following Python program runs in 194ms. (Internal runtime is 125ms).
Run: [ @replit ]
from enigma import (SubstitutedExpression, multiply, ndigits, group, unpack, printf) # find possible sets of 3 numbers, their product and number of digits # return (<numbers>, <product>) def generate(): # find two 3-digit primes, using different digits p = SubstitutedExpression( ["is_prime(ABC)", "is_prime(DEF)", "A < D"], answer="(ABC, DEF, GHIJ)", ) for ns in p.answers(verbose=0): p = multiply(ns) yield (ns, p) # group candidates by (<digit length>, <parity>) of the product g = group(generate(), by=unpack(lambda ns, p: (ndigits(p), p % 2))) # look for candidate sets that are unique by (<digit length>, <parity>) of the product for ((k, m), vs) in g.items(): if len(vs) != 1: continue # check there are solutions of the other parity if not g.get((k, 1 - m)): continue # output solution (ns, p) = vs[0] printf("{k} digits -> parity {m} -> {ns} = {p}")Solution: The three numbers are: 109, 367, 2485.
The product is 99407455, which is 8-digits long. But there are 15 different products that are 8 digits long, so we cannot tell which set of numbers we started with, knowing only the number of digits in the product.
However there is only one 8-digit product that is odd, and only one set of numbers that gives this product, and so provides the answer to the puzzle.
LikeLike
Jim Randell 9:37 am on 20 July 2024 Permalink |
In fact it enough to know the solution is unique by (<digit length>, <parity>) of the product. There is only a single candidate, so the additional check that the digit length alone is not sufficient to determine the product is not required (although a complete solution should verify it).
But this leads to a shorter program:
from enigma import ( SubstitutedExpression, multiply, ndigits, filter_unique, unpack, printf ) # find possible sets of 3 numbers, their product and number of digits # return (<numbers>, <product>) def generate(): # find two 3-digit primes, using different digits p = SubstitutedExpression( ["is_prime(ABC)", "is_prime(DEF)", "A < D"], answer="(ABC, DEF, GHIJ)", ) for ns in p.answers(verbose=0): p = multiply(ns) yield (ns, p) # answer is unique by (<digit length>, <parity>) of product f = unpack(lambda ns, p: (ndigits(p), p % 2)) for (ns, p) in filter_unique(generate(), f).unique: # output solution printf("{k} digits -> parity {m} -> {ns} = {p}", k=ndigits(p), m=p % 2)LikeLike
Frits 5:52 pm on 19 July 2024 Permalink |
from itertools import permutations # prime numbers between 101 and 1000 with different digits P = [3, 5, 7] P += [x for x in range(11, 100, 2) if all(x % p for p in P)] P = [str(x) for x in range(101, 1000, 2) if all(x % p for p in P) and len(set(str(x))) == 3] # product of two 3-digit numbers and a 4-digit number has length 8, 9 or 10 impossible = {8: 0, 9: 0, 10: 0} d, dgts = dict(), set("0123456789") # choose two prime numbers for i, p1 in enumerate(P[:-1]): for p2 in P[i + 1:]: # different digits if len(s12 := set(p1 + p2)) != 6: continue p1_x_p2 = int(p1) * int(p2) # break if for high products we can never work out all the three numbers if impossible[9] and impossible[10] and p1_x_p2 > 99999: break # consider all variants of the third number for p in permutations(dgts - s12): if (n3 := int(''.join(p)) ) < 1000: continue # check if we already have enough entries for this (length, parity) if impossible[ln := len(str(prod := p1_x_p2 * n3))]: continue # store length/parity d[(ln, par)] = d.get((ln, par := prod % 2), []) + [(p1, p2, str(n3))] # if a length for both parities already has 2 entries or more # then remember this for subsequent processing if all((ln, par) in d and len(d[(ln, par)]) > 1 for par in [0, 1]): impossible[ln] = 1 # check all possible solutions for (ln, par), vs in d.items(): # no uniqueness? if impossible[ln]: continue # can we work out all the three numbers? if len(vs) == 1 and (ln, 1 - par) in d: print("answer:", ', '.join(vs[0]))LikeLike
GeoffR 12:16 pm on 20 July 2024 Permalink |
Trial testing showed that there were 8, 9 or 10 digits in the product of the three numbers.
from itertools import permutations from enigma import is_prime from collections import defaultdict dlen = defaultdict(list) key = 0 for p1 in permutations('1234567890'): A, B, C, D, E, F, G, H, I, J = p1 if '0' in (A, D, G):continue ABC = int(A + B + C) if not is_prime(ABC):continue DEF = int(D + E + F ) if D < A:continue if not is_prime(DEF):continue GHIJ = int(G + H + I + J) # product of two primes and a 4-digit number prod = ABC * DEF * GHIJ # Classify products for length and parity # Assume the products are 8, 9 or 10 digit in length if len(str(prod)) == 8 and prod % 2 == 0: key = 1 if len(str(prod)) == 8 and prod % 2 == 1: key = 2 if len(str(prod)) == 9 and prod % 2 == 0: key = 3 if len(str(prod)) == 9 and prod % 2 == 1: key = 4 if len(str(prod)) == 10 and prod % 2 == 0: key = 5 if len(str(prod)) == 10 and prod % 2 == 1: key = 6 # update dictionary dlen[key] += [ (prod, (ABC, DEF, GHIJ))] for k, v in dlen.items(): # Answer is a single entry in dictionary if len(v) == 1: print('Ans = ', k, v) # find number of products in each group if k == 1: print(k, len(v)) if k == 2: print(k, len(v)) if k == 3: print(k, len(v)) if k == 4: print(k, len(v)) if k == 5: print(k, len(v)) if k == 6: print(k, len(v))LikeLike
Ruud 2:23 pm on 20 July 2024 Permalink |
Quite similar to @Frits, just a it more brute force.
from istr import istr from collections import defaultdict def is_prime(n): if n < 2: return False if n % 2 == 0: return n == 2 k = 3 while k * k <= n: if n % k == 0: return False k += 2 return True collect = defaultdict(list) for n1 in istr(range(100, 988)): if not is_prime(int(n1)): continue if not n1.all_distinct(): continue for n2 in istr.range(n1 + 1, 988): if not is_prime(n2): continue if not (n1 | n2).all_distinct(): continue for n3 in istr.concat(istr.permutations((c for c in istr.digits() if c not in n1 | n2))): if n3 < 1000: continue product = n1 * n2 * n3 collect[len(product), product.is_odd()].append((n1, n2, n3)) for v in collect.values(): if len(v) == 1: print(*map(int, v[0]))LikeLike